Obvod elipsy

Obvod elipsy lze vypočítat buď pomocí přibližných vzorců nebo jako částečný součet nekonečné řady. K dispozici je vícero nekonečných řad, zde byla pro výpočty použita následující řada, ktera dosti rychle konverguje: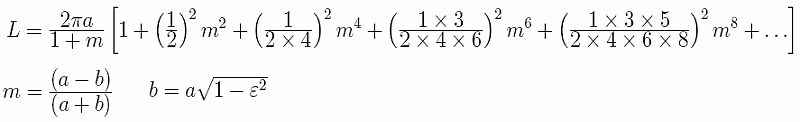

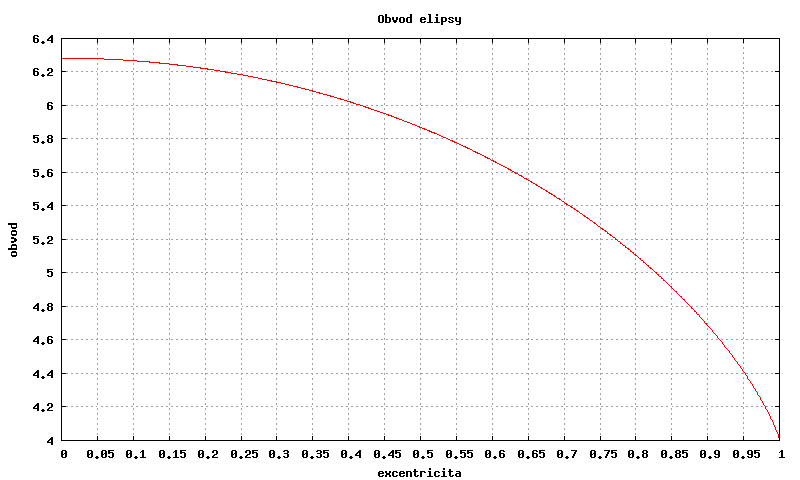
Graf závislosti délky obvodu elipsy na excentricitě (ε), velká poloosa je rovna 1 (a=1): Zvláštní případy:
Je-li ε = 0, je obvod 2π a blíží-li se ε zdola k 1, blíží se obvod shora k 4.

Tabulky:
Zde uvedené tabulky pro obvod elipsy mají velkou poloosu vždy rovnu 1 (a=1) a délka obvodu elipsy je vypočtena pro různé hodnoty excentricity (ε):
Tabulka hodnot obvodu elipsy na 100 desetinných míst pro excentricitu 0.00 až 0.99 po 0.01
(download, 1 strana PDF, 32 KiB)
Tabulka hodnot obvodu elipsy na 8 desetinných míst pro excentricitu 0.0000 až 0.9999 po 0.0001
(download, 10 stran PDF, 115 KiB)

---

Kontakt na autora: